IMU und Robotertechnik: Was Sie wissen sollten

 

IMU und Robotertechnik: Was Sie wissen sollten

In diesem Artikel finden Sie zahlreiche Informationen, die es beim Kauf Ihrer IMU je nach Anforderungsprofil zu beachten gilt.

Sie werden erfahren, wie eine IMU funktioniert und wie ihre Parameter ausgewertet werden können. Am Ende des Artikels finden Sie ebenfalls mehrere Links zu Tests und anderen Ressourcen.

Definition – Was ist eine IMU?

Eine inertiale Messeinheit (engl. Inertial Measurement Unit, IMU) ist ein elektronisches Bauteil, das zur Gruppe der Sensoren gehört. Damit wird die Beschleunigung des Sensors, die Winkelgeschwindigkeit und Orientierung mithilfe einer Kombination aus Beschleunigungsmessern,

Gyroskopen und Magnetometern gemessen. Die IMU vom Typ I umfasst Beschleunigungsmesser und Gyroskope, während die IMU vom Typ II zusätzlich Magnetometer aufweist. Die Beschleunigungsmesser, Gyroskope und Magnetometer dienen zur Messung von Daten auf einer einzigen Achse (X: Nick, Y: Roll, Z: Gier).

Um Informationen für die 3 Achsen zu erhalten, müssen jeweils drei Bauteile jedes Geräts (d. h. von Beschleunigungsmessern, Gyroskopen und Magnetometern) integriert werden, um eine IMU vom Typ II zu erhalten. Ein typischer IMU-Sensor umfasst 9 Freiheitsgrade (DoF) mit:

• 3 Beschleunigungsmessern
• 3 Gyroskopen
• 3 Magnetometern

Bestimmte IMU können zusätzliche Freiheitsgrade über einen Temperatursensor, GPS-Sensor, Drucksensor usw. aufweisen. Basierend auf der Beschleunigung können Berechnungen zur Lagebestimmung, von Geschwindigkeit und Position durchgeführt werden.

Mit den Gyroskopen kann die Winkellage ermittelt werden. Diese Daten der IMU sind unerlässlich für die mobile Robotertechnik. Sie ergänzen somit die Messungen der LiDAR sowie die odometrischen Messungen.

Unser Angebot an Gyroskopen und Inertialsensoren ansehen

Physikalische Grundlagen – Wie funktioniert eine IMU?

Um zu verstehen, wie eine IMU funktioniert, müssen zunächst alle Unterkomponenten analysiert werden:

Unterkomponente 1: Beschleunigungsmesser

Ein Beschleunigungsmesser ist ein elektromechanisches Gerät, das zur Messung von Beschleunigungskräften dient. Diese Kräfte sind:

• Statisch, wie die Schwerkraft; oder
• Dynamisch, wie die Bewegungs- oder Schwingungskräfte.

Die Beschleunigung entspricht der Messung der Geschwindigkeitsvariation oder der Geschwindigkeit geteilt durch die Zeit. Zum Beispiel: Ein Fahrrad, das aus dem Stillstand innerhalb von fünf Sekunden auf 30 km/h beschleunigt wird, besitzt eine Beschleunigung von 6 km/h pro Sekunde (30 geteilt durch 5).

Unterkomponente 2: Gyroskop

Ein Gyroskop ist ein Gerät zur Messung oder Beibehaltung von Orientierung und Winkelgeschwindigkeit. Es handelt sich um ein sich drehendes Rad oder eine Scheibe, bei dem/der sich die Rotationsachse selbstständig jede beliebige Orientierung annehmen kann.

Bei der Drehung wird die Orientierung dieser Achse durch die Neigung oder Drehung des Trägers je nach Beibehaltung des Drehimpulses nicht beeinflusst.

Unterkomponente 3: Magnetometer

Ein Magnetometer ist ein Gerät zur Messung des Magnetismus:

• Anziehungsrichtung
• Anziehungskraft
• Relative Änderung eines Magnetfelds zu einem gegebenen Standort

Der Kompass ist beispielsweise ein derartiges Gerät, mit dem die Richtung eines umgebenden Magnetfelds gemessen werden kann. Im vorliegenden Fall das Erdmagnetfeld.

ROS – Datenübertragung von der IMU

Alle ROS-kompatiblen IMU-Sensoren geben ihre Daten im Topic /imu im Nachrichtenformat sensor_msgs/Imu.msg aus:

std_msgs/Header header geometry_msgs/Quaternion orientation float64[9] orientation_covariance geometry_msgs/Vector3 angular_velocity float64[9] angular_velocity_covariance geometry_msgs/Vector3 linear_acceleration float64[9] linear_acceleration_covariance

Orientierung

Die 3D-Rotationen und die Orientierung können unter Verwendung der Form der Euler-Winkeln oder in Form von Quaternionen dargestellt werden.

Euler-Winkel

Die Euler-Winkel bestehen aus drei Winkelwerten für die X-, Y- und Z-Achse. Jeder Rotationswert wird sequenziell, das heisst aufeinanderfolgend, angewendet. Vorteile Die Euler-Winkel verfügen über ein intuitives Format, das „mit blossem Auge“ lesbar ist.

Nachteile Bei einigen Konfigurationen kommt es bei Euler-Winkeln zu einem Verlust von Freiheitsgraden. Bei aufeinanderfolgender Anwendung von drei Rotationen kann es vorkommen, dass aufgrund der ersten oder zweiten Drehung die dritte Achse in dieselbe Richtung zeigt wie einer der anderen beiden Achsen, sodass der dritte Rotationswert nicht um eine Einzelachse angewendet werden kann.

Quaternionen

Quaternionen können verwendet werden, um die Orientierung oder Rotation eines Objektes darzustellen. Die Darstellung umfasst vier Zahlen (in der Einheit referenziert als x, y, z und w). Sie sollten nicht vergessen, dass mit diesen Grössen keine Winkel oder Achsen dargestellt werden und dass Sie normalerweise nie direkt darauf zugreifen müssen.

Vorteile Bei Quaternion-Rotationen kommt es zu keinem Verlust an Freiheitsgraden. Nachteile Eine einzige Quaternion kann in keine Richtung eine Rotation von über 180° darstellen und ist intuitiv nicht verständlich.

Winkelgeschwindigkeit

Die Winkelgeschwindigkeit wird durch einen dreidimensionalen Vektor (x, y und z) dargestellt und die Winkelgeschwindigkeitswerte sind von der x-, y- und z-Achse abhängig.

Lineare Beschleunigung

Die lineare Beschleunigung wird durch einen dreidimensionalen Vektor (x, y und z) dargestellt und die linearen Beschleunigungswerte sind von der x-, y- und z-Achse abhängig.

Kovarianz

Bei den Sensoren ist die Kovarianz der Vertrauenskoeffizient für die Genauigkeit des Sensors. Die Kovarianz kann je nach Sensorleistung statisch sein oder kontinuierlich aktualisiert werden, wobei sie sich im Laufe der Zeit in Abhängigkeit von der Schätzung der Genauigkeit ändert.

Dasselbe gilt für die IMU, die eine statische oder dynamische Kovarianz aufweisen kann. Jeder Parameter besitzt einen zugewiesenen Kovarianzkoeffizienten, der fest eingestellt oder mit der Sensorsoftware verarbeitet wird, wobei somit anzeigt wird, wie zuverlässig der Wert sein kann.

Übersicht über die Eigenschaften der IMU

Energieverbrauch

Um den Energiebedarf für Ihr Roboterprojekt festzulegen, muss die Betriebsart und Betriebsdauer Ihrer Ausrüstung mitberücksichtigt werden. Diese Parameter sind wichtig, wenn der Sensor mit einer Batterie betrieben wird:

• Versorgungsspannung in Volt
• Betriebsstrom in Ampere
• Leistung in Watt

Kenndaten des Sensors

Die digitale Auflösung beschreibt das gesamte Detektionsvermögen Ihres Sensors und umfasst zwei Bereiche: 1. Abstand => Bewegungsmenge, die die Sensoren berücksichtigen können:

• Bei einem Beschleunigungsmesser wird dieser Wert in G-Kraft gemessen.
• Die Gyroskope werden je nach Geschwindigkeit der Winkelrotation, die sie quantitativ in Grad/Sekunde erfassen können, eingeteilt.
• Die Magnetometer messen ihre Kapazität in µT, die je nach Sensorachse (x, y, z) variieren kann.

2. Empfindlichkeit => Absolute Zahl, die die kleinste Menge an messbaren und erfassbaren Änderungen darstellt. Bei den Sensoren hängt dies unmittelbar mit der für den jeweiligen Sensor reservierten Bitanzahl zusammen. Je mehr Bits vorhanden sind, desto höher ist die Empfindlichkeit. Null-Gravitations-Offset: Wert des Beschleunigungsmessers, wenn keine äussere Kraft angewendet wird.

Entspricht dem kleinsten erfassten Fehler. Nullpegel-Offset: Wert des Gyroskops bei fehlender Winkelbewegung, was von der Temperatur abhängig sein kann. Datendurchsatz: Anzahl der durchgeführten Messungen im Laufe eines gegebenen Zeitintervalls.

Wenn Sie Ihre IMU auswählen, stellen Sie sicher, dass die Pegel der berücksichtigten Sensoren mit den Anforderungen Ihrer Anwendungen übereinstimmen. Rauschdichte: Definiert als Einheit pro Quadratwurzel der Bandbreite, typischerweise:

• ug/sqrt(Hz) für Beschleunigungsmesser
• deg/sqrt(Hz) für Gyroskope

Bandbereich: Der Frequenzbereich, in dem ein Beschleunigungsmesser oder ein Gyroskop betrieben wird. Schnittstellen: Welches Kabel und Kommunikationsprotokoll werden von der IMU und Ihrem mitgeführten System genutzt?

Temperaturbereich: Die minimalen und maximalen Umgebungstemperatursonden können sicher funktionieren, um genaue Messungen zu liefern.

Ausgangsparameter

Statische Genauigkeit: Genauigkeit am Ausgang des Sensors, wenn das Gerät relativ stabil/immobil ist. Dynamische Genauigkeit: Genauigkeit am Ausgang des Sensors, wenn das Gerät in Bewegung ist. Rotationsfehler: Unterschied zwischen dem Ausgangsvektor und dem realen Vektor, gemessen in Grad.

Heading Error: Unterschied zwischen dem Ausgang der Gierachse und dem realen Wert, gemessen in Grad. Heading Drift: Fehleranhäufung im Laufe der Zeit. RAW Accel/Gyro/Mag: Bruttoausgangswert jedes Sensors vor der Verarbeitung.

Calibrated Accel/Gyro/Mag: Ausgangswert jedes Sensors nach Verwendung der Sensorfusion zur Verarbeitung und Bereinigung jedes Signals.

Kalibrierung

Nach Prüfung der Parameter am Sensorausgang gibt es noch einen weiteren Faktor, den Sie berücksichtigen sollten: die Kalibrierung. Die Kalibrierungsoptionen, die Sie aussuchen, sind von Ihrem Budget und den Anforderungen Ihres Projektes abhängig. Nach Prüfung der Parameter am Sensorausgang gibt es noch einen weiteren Faktor, den Sie berücksichtigen sollten: die Kalibrierung. Die Kalibrierungsoptionen, die Sie aussuchen, sind von Ihrem Budget und den Anforderungen Ihres Projektes abhängig.

Nominal: Die nominale Kalibrierung nutzt Durchschnittswerte für den Sensor, um eine Durchschnittsleistung zu liefern.

Per-device: Die Kalibrierung nach Gerät ermöglicht, bestimmte Parameter zu kalibrieren, wie Sensorverstärkung, die für jedes Bauteil einen eigenen Wert aufweist. Je nach Anwendung können Sie sich entscheiden, eine Kalibrierung über eine Einzelachse oder über mehrere Achsen für Ihr Projekt vorzunehmen. Dynamisch: Wenn Sie der Meinung sind, dass die nominale Kalibrierung akzeptabel ist, kann der Ausgang Ihres Sensors in der Praxis zusätzlich dynamisch korrigiert werden.

Die Eigenschaften des Sensors variieren je nach Temperatur und können im Laufe der Verwendung des Sensors in seiner Endanwendung weiter angepasst werden.

Algorithmen zur Datenfusion

Der Kalman-Filter

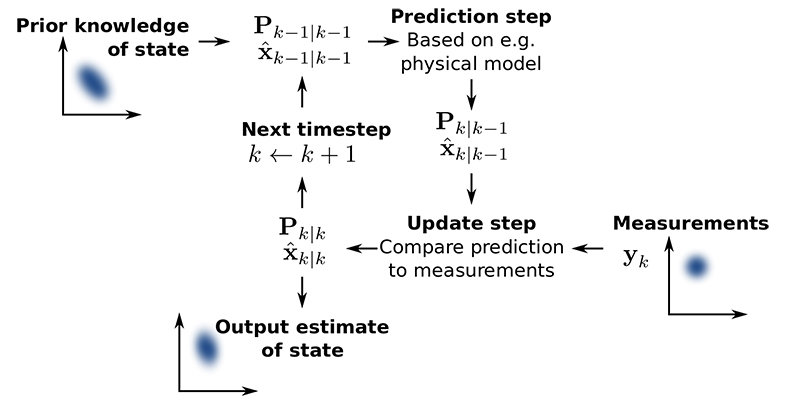
Der Kalman-Filter ist eine Modellimplementation:

• Zunächst stellt der Filter auf der Grundlage seines Modells eine Hypothese für den nächsten Ausgangswert des Sensors auf.
• Anschliessend nimmt er den gemessenen Wert und vergleicht ihn mit dem angenommenen Wert.
• Abschließend aktualisiert er sein Modell, um genauere Hypothesen für die nächste Messung aufzustellen.

Mit jeder Datensequenz aus den Sensoren wird das Modell statistisch verbessert, um die Ausgangswerte zu berechnen. Gleichzeitig wird ebenfalls die Genauigkeit der Sensoren bewertet.

Das Modell hängt vom Fehler des Sensors und der jeweiligen Anwendung ab. Für die mobilen Robotiksysteme wissen wir aufgrund der Kenntnisse aus der realen Welt, dass sich die physischen Objekte langsam und stetig im Raum bewegen anstatt in den Raum teleportiert zu werden, wie Stichproben von GPS-Koordinaten angeben könnten.

Dies bedeutet, dass, wenn ein Sensor, der immer ausgezeichnete Werte auf konstante Weise angezeigt hat, beginnt, unwahrscheinliche Ereignisse anzugeben (wie die GPS-/Funksysteme in einem Tunnel), das Glaubwürdigkeitsmaß des Sensors nach einigen Wiederholungen von einigen Millisekunden sinkt, bis er wieder beginnt, zusammenhängende Werte zu messen.

Dies ist besser als die einfache Berechnung des Durchschnittswerts, da der Kalman-Filter die meisten seiner Sensoren unterstützen kann, die vorübergehend ungenau werden. Man braucht zumindest einen Sensor, der relativ genaue Wert überträgt. Er stellt die gute Funktionsweise des Roboters sicher, bis die anderen Sensoren wieder funktionieren.

Der Kalman-Filter ist eine Anwendung der allgemeineren Konzepte der mathematischen Systeme Markov-Kette und Bayessche Interferenz, die ihre Annahmen schrittweise mithilfe von Beweisen verfeinern.

PID-Filter

Die einfacheren Robotiksysteme können mit PID-Filtern ausgestattet sein. Man kann sie als einfache Kalman-Filter betrachten, die durch einen einzigen Sensor versorgt werden, wobei alle schrittweisen Einstellungen wegfallen und durch drei feste Werte (kp, ki und kd) ersetzt werden.

Es handelt sich um ein Korrektursystem, dass den Eingangswert durch die Kontrollschleife anpasst, um einen guten Ausgangswert zu erhalten. Auch wenn die PID-Werte automatisch oder manuell eingestellt werden, ist der gesamte „Einstellungsprozess“ (anpassen, fliegen, bewerten, wiederholen) eine ausgelagerte Version des Kalman-Filters mit einem Menschen, der die Belief-Propagation-Phase übernimmt.

Personalisierte Filter

Die richtigen Systeme sind oft hybrid, zwischen diesen beiden Möglichkeiten.

ROS-Pakete für IMU

Wenn Sie Ihre Roboter-Software unter ROS installieren, ist es einfacher, ROS-kompatible Sensoren zu kaufen. Das heißt, dass die Hersteller bereits ein ROS-Paket entwickelt haben, um eine Interaktion des Sensors unter ROS zu ermöglichen. So gewinnen Sie Zeit.

Was die IMU betrifft, so werden mit dem Sensor Rohdaten oder verarbeitete Daten je nach Implementierungskonfiguration Ihrer IMU im Topic /imu ausgegeben. Anschliessend können Sie sich unter ROS bei diesem Topic anmelden, um Daten zu erhalten, die Sie beispielsweise für die Navigation verwenden können. Einige der ROS-Pakete sind bereits implementiert und aktualisiert:

• imu_transformer : Dieses Paket stellt eine Kombination aus Nodes/Nodelets bereit, die verwendet werden können, um die IMU-Daten aus einem TF-Raster in ein anderes umzuwandeln.
• imu_tools :
  • Imu_filter_madgwic : Filter zur Fusion der Winkelgeschwindigkeiten, Beschleunigungen und magnetischen Auslesevorgänge (optional) einer generischen IMU-Vorrichtung mit einer Orientierung auf der Basis des Algorithmus nach Sebastian Madgwick.
  • Imu_complementary_filter : Filter zur Fusion der Winkelgeschwindigkeiten, Beschleunigungen und magnetischen Auslesevorgänge (fakultativ) einer generischen IMU-Vorrichtung in einer Quaternion zur Darstellung der Orientierung der Vorrichtung im globalen Raster auf der Basis des Algorithmus nach Roberto G. Valenti.
  • rviz_imu_plugin: Ein Plugin für rviz mit Anzeige von sensor_msgs::Imu messages
• imu_utils : Paket zur Überwachung der Leistungen der IMU in Matlab

Wie wird die IMU am besten ausgewählt?

• Integrated computations
• Integrated filters
• Embedded microcontroller
• Board library (Arduino, Raspberry pi, etc.)
• ROS compatibility
• Interface

Treffen Sie eine Wahl je nach Anforderungen Ihres Projektes. Die kostengünstigste IMU liefert nur Bruttowerte, während UM7 die verarbeiteten Werte filtert und direkt in einer ROS-Nachricht ausgibt.

Auch die teuersten IMU weisen relativ ähnliche Leistungen auf. Der Unterschied besteht in den angebotenen Services und zusätzlichen Implementierungsmöglichkeiten:

• Integrierte Berechnungen
• Integrierte Filter (sehr leistungsfähig: die IMU von SBG Systems )
• Integrierter Microcontroller
• Bordbibliothek (Arduino, Raspberry pi, etc.)
• ROS-Kompatibilität
• Schnittstelle
• Integration mit GPS Daten ( Inertialeinheit Ellipse 2 Micro INS )

Welche Leistungen bietet eine IMU?

Ein IMU-Sensor ist ein nützliches Bauteil, das in Ihren Roboter eingesetzt werden kann. Es liefert Informationen zu Winkellage, Orientierung, Position, Geschwindigkeit, Beschleunigung, Rotationsgeschwindigkeit, wenn die Werte berechnet werden. Sie sollten jedoch nicht vergessen, dass die IMU Driftfehlern unterliegt.

Die Fehler häufen sich im Laufe der Zeit, da die neuen Werte auf den vorherigen Werten basieren. Zudem kann die IMU, die ein Magnetfeld zur Berechnung der Werte nutzt, durch andere Magnetfelder (Motor, Metallstruktur usw.) beeinträchtigt werden, die zu enormen Fehlern führen können. Sie können Korrekturen und Filter implementieren, um diese Fehler zu reduzieren, aber der IMU-Fehler wird abdriften und kontinuierlich ansteigen.

Eine Möglichkeit, dieses Problem zu lösen, besteht darin, den Kovarianzwert (Vertrauenskoeffizienten) zu berücksichtigen, der sich im Laufe der Zeit verändern kann, wenn es ein dynamischer Wert ist.

Eine andere Möglichkeit ist, einen GPS-Sensor hinzuzufügen. Das GPS-Signal kann den IMU-Wert aktualisieren und den Driftfehler korrigieren. Für greifbare Ergebnisse gibt Ihnen ein Online-Visualisierungstest von IMU- und EMG-Sensor-Daten zur Auswertung einer Handgelenksbelastung eine Übersicht über den Fehler einer IMU (Abschnitt 2.1 und 3.1).

In einem anderen Artikel werden alle systematischen Verzerrungen der IMU, die zu Fehlern führen , aufgelistet und beschrieben. Hier finden Sie eine schnelle und effiziente Methode, um eine IMU zu bewerten.

Schlussfolgerung: Vorteile und Nachteile der IMU

Vorteile einer IMU

1. Das Trägheitsnavigationssystem ist unabhängig von externen Informationen und verbraucht nicht viel Energie.
2. Das Trägheitsnavigationssystem kann über Standort, Geschwindigkeit, Winkellage, Winkeldaten informieren, und die anschliessenden Navigationsinformationen erfolgen kontinuierlich.
3. Hochfrequenzmessung und gute Stabilität.

Nachteile einer IMU

1. Aufgrund der Informationen des integrierten Navigationssystems steigt der Positionsfehler im Laufe der Zeit an und gewährleistet nur eine langfristig geringe Präzision.
2. Eine lange Angleichungszeit zu Beginn ist vor jeder Nutzung notwendig.
3. Es können keine Zeitangaben geliefert werden.